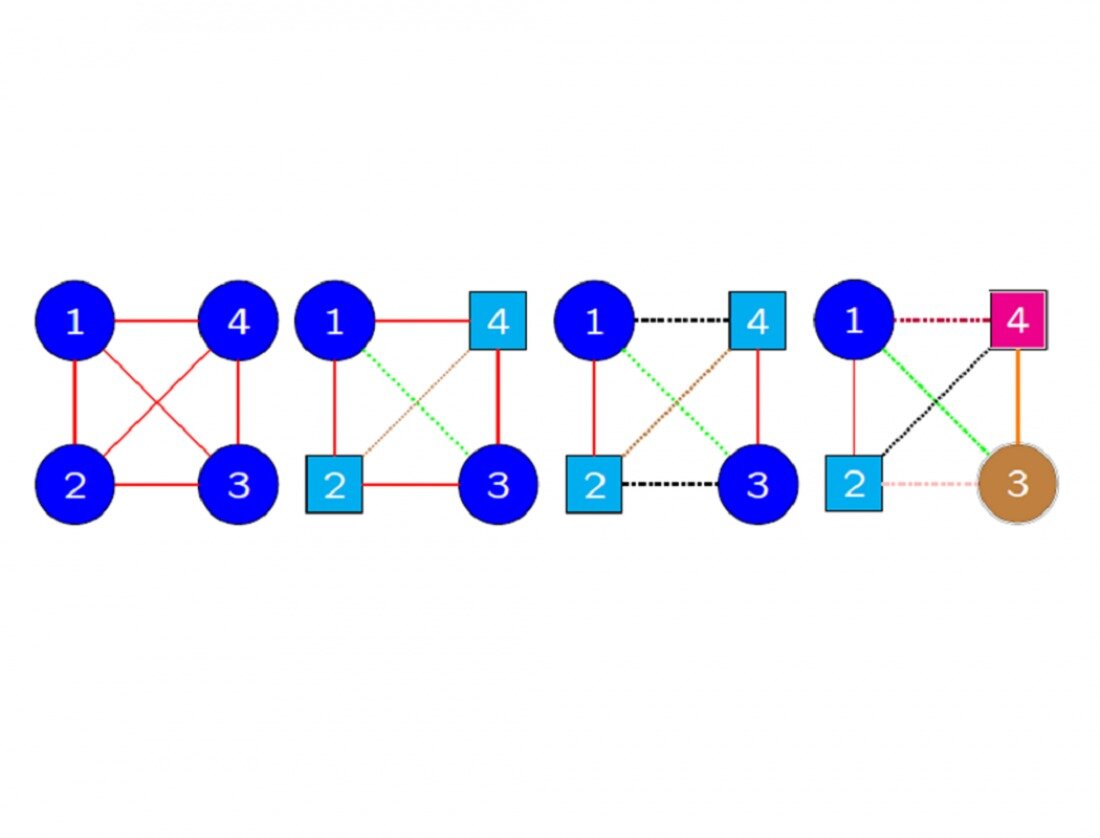
Examples of colored charts denoting symmetries of four-dimensional data: Vertices and edges of the same color and shape in a chart are mapped onto one another by a symmetry permutation, while preserving the structure of the data. Photo credit: Hideyuki Ishi, Osaka Metropolitan University
An international research team led by scientists from Osaka Metropolitan University has developed a method to identify symmetries in multidimensional data using Bayesian statistical techniques.
This statistical approach requires complex calculations of integrals, which are often only considered as approximations. In their new study, the research team successfully derived new exact integral formulas. Their results will help improve the accuracy of data symmetry identification methods and potentially expand their applications to broader areas of interest such as genetic analysis.
Symmetries in nature make things beautiful; Symmetries in data make data processing efficient. However, the complexity of identifying such patterns in data has always plagued researchers. Scientists from Osaka Metropolitan University and their colleagues have taken a major step towards detecting symmetries in multidimensional data using Bayesian statistics. Their results were published in The annals of statistics.
Bayesian statistics has been in the spotlight in recent years due to improvements in computing power and their potential applications in artificial intelligence. Bayesian statistics is a statistical approach that, even when data is insufficient, infers the probability of an event occurring by first establishing a prior probability and then, whenever new information becomes available, a later probability—an update of the previous probability – calculated that the event will occur. The calculation of posterior probabilities requires complex calculations of integrals and is therefore often considered only an approximation.
The international team, which includes Professor Hideyuki Ishi from Osaka Metropolitan University, Professor Piotr Graczyk from the University of Angers, Professor Bartosz Kołodziejek from Warsaw University of Technology and the late Professor Hélène Massam from York University (Toronto), is succeeded in deriving new exact integral formulas, and in developing a method for searching for symmetries in multidimensional data using Bayesian statistical techniques.
As the amount of data to be handled increases, the optimal pattern must be selected from a large number of patterns, making it difficult to solve the problem accurately. To address this challenge, the team also developed an efficient algorithm to get an approximate solution even in such cases.
In the words of Professor Ishi: “Symmetries in data are ubiquitous in a variety of models. Once symmetries are identified, the number of parameters required to represent the structure of the data and the number of samples required to determine the parameters can be significantly reduced. In the future, the results of this research should contribute to genetic analysis to discover chromosomes that have the same function in different places.”
Bayesian model selection shows extremely polarized behavior when the models are wrong
Piotr Graczyk et al, Model selection in the space of symmetry-invariant Gaussian models, The annals of statistics (2022). DOI: 10.1214/22-AOS2174
Provided by Osaka Metropolitan University
Citation: New Method for Identifying Symmetries in Data Using Bayesian Statistics (2022 September 13) Retrieved September 13, 2022 from https://phys.org/news/2022-09-method-symmetries-bayesian-statistics. html
This document is protected by copyright. Except for fair trade for the purpose of private study or research, no part may be reproduced without written permission. The content is for informational purposes only.
#method #identify #symmetries #data #Bayesian #statistics

Leave a Comment